- Record: found
- Abstract: not found
- Book Chapter: not found
Artificial Neural Networks and Machine Learning – ICANN 2018
Using Regular Languages to Explore the Representational Capacity of Recurrent Neural Architectures
other
Read this book at
There is no author summary for this book yet. Authors can add summaries to their books on ScienceOpen to make them more accessible to a non-specialist audience.
Related collections
Most cited references9
- Record: found
- Abstract: not found
- Article: not found
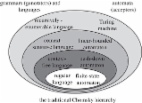
On certain formal properties of grammars
Noam Chomsky (1959)
- Record: found
- Abstract: found
- Article: found
Artificial grammar learning meets formal language theory: an overview
W. Tecumseh Fitch, Angela Friederici (2012)
